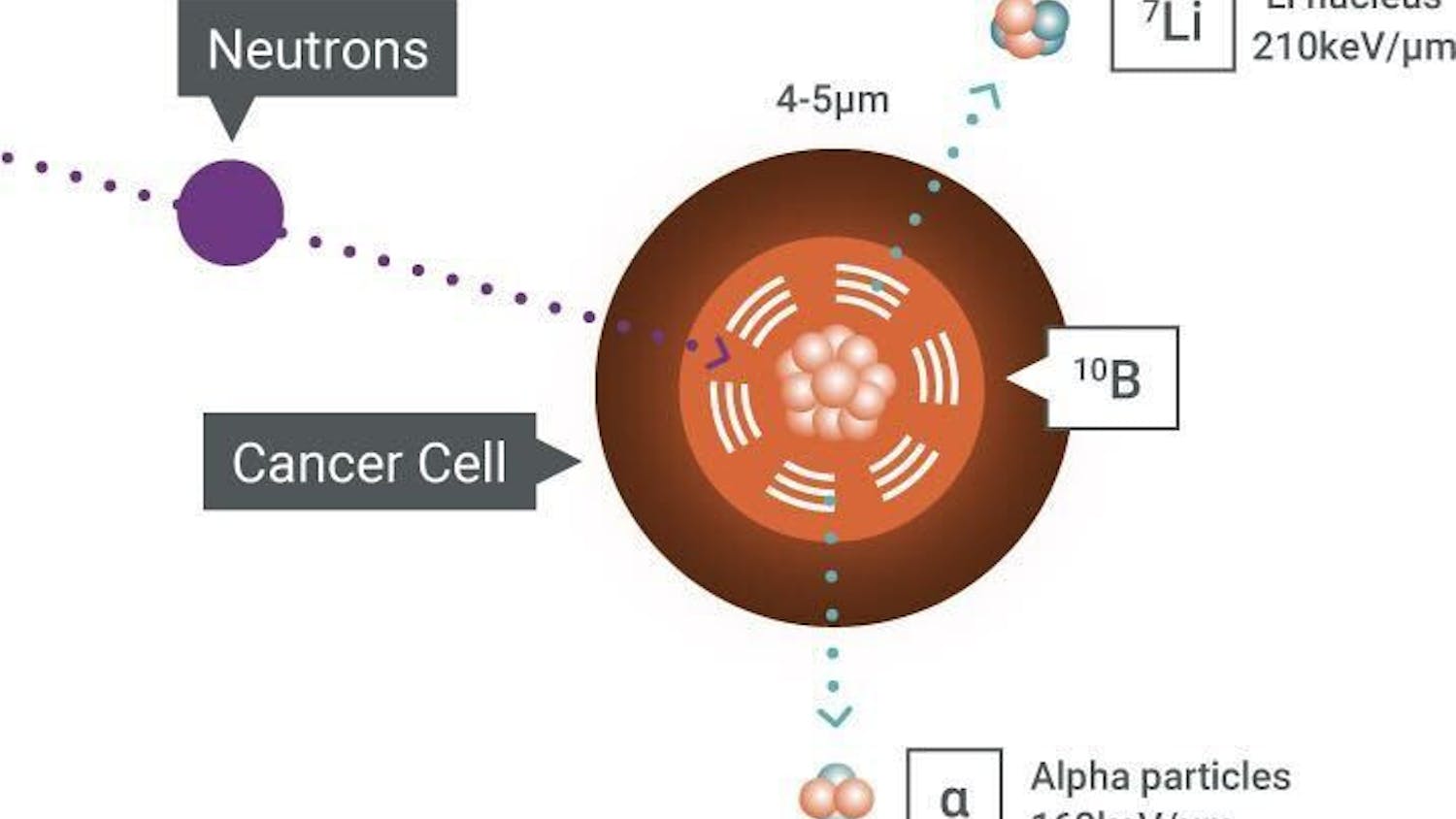
For the first time in almost 10 years, quantum mechanics reappeared as the inspiration behind the Nobel Prize in Physics. In recognition of their work on quantum entanglement, this year’s highly esteemed physics award was split three ways between physicists Alain Aspect, John Clauser and Anton Zeilinger.
Quantum entanglement — a unique subatomic phenomenon that links the properties of two seemingly noninteracting particles — defies all known intuitions of our macroscopic world. This bizarre behavior, along with its connection to real-world applications such as quantum computing and communication, has led quantum entanglement to capture the minds of amateurs and experts alike.
This newly announced Nobel Prize marks the next chapter in this field.
All three awardees were involved in designing and performing various experiments that deepened our understanding of quantum entanglement. Zeilinger, a professor of physics at the University of Vienna and designer of the most recent set of experiments, was interested in understanding a peculiar side effect of quantum entanglement called quantum teleportation. In essence, Zeilinger’s experiments showed that, through using two entangled particles, information could be shared over arbitrary distances, paving the way for a potentially highly secure commercial quantum network.
Zeilinger’s experiments were only possible because of the experiments performed by Clauser, a researcher at J.F. Clauser & Associates, and Aspect, a professor at the University of Paris-Saclay’s Institut d’Optique Graduate School. Both physicists independently worked to design an instrument that could analyze the presence of quantum entanglement. Clauser was the first of the two — having begun his tests in the 1970s.
Clauser received promising results, but problems persisted. Ten years later, Aspect was successful in eliminating the remaining issues via an upgraded version of Clauser’s original experiment.
While this may have been the extent of this year’s Nobel Prize in Physics, it only constitutes the most recent strokes on a much larger picture of quantum entanglement.
To get to the beginning of this story, one needs to travel back in time to the mid-1930s. It had only been 10 years since the field of quantum mechanics was even theorized. The novelty and uniqueness of quantum mechanics led any discussion around the subject to rip through the physics community like wildfire. Naturally, given the time period and topic, Albert Einstein worked his way to the middle of this discourse.
Throughout the early 1930s, Einstein would publish a smattering of papers discussing the various intricacies of quantum mechanics. However, it was in 1935 that Einstein would publish one of his most influential quantum mechanics papers. Teaming up with contemporary physicists Boris Podolsky and Nathan Rosen, the three released a paper under the provocative title, “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?”
As the title may suggest, Einstein and his colleagues argued that certain “physical irregularities” seemed so wild and out of the ordinary that the only logical conclusion is that quantum mechanics must be incomplete. The most obvious of these irregularities? Quantum entanglement.
Einstein, Podolsky and Rosen (EPR) set up their thought experiment by first using the notion of the uncertainty principle — a famous interpretation which shows that for a given particle one could only know either its position or momentum with absolute certainty, not both, as measuring one would alter the other. Using this, the physicists then established the idea of non-commutability between two particles.
Put simply, two operators — for instance, X and Y — are non-commutable when XY≠YX. It can be useful to think of these operators as “actions” being performed on something. In a mathematical context, these operators act on wavefunctions — the equations that represent atomic particles — to produce unique numerical results. However, real-world analogies, like the uncertainty principle, are also useful for highlighting this same idea.
By replacing X and Y with the act of measuring location and momentum respectively, it becomes reasonable to argue that for a single particle these two actions are not commutable. For instance, if we measured the momentum of a particle, the act of doing so would send it flying off in a different direction, giving a location different from its original starting point when measured. If we had instead measured the position first, it would be detected in its unaltered starting point, already showing the inequality between XY and YX.
To supporters of quantum mechanics at the time, this idea was solid. What made the EPR paper so shocking was that they were able to show, through a little bit of math, that in a quantum mechanical framework standard physics starts to break down. It would seem that “two physical quantities, with non-commuting operators, can have simultaneous realities,” describe Einstein and his co-authors. That is to say, two quantities whose very interactions should envelop them in a cloud of uncertainty are somehow linked, or rather entangled, in such a way that knowing one, predictably changes the other.
Theoretically, if two people at opposite ends of the universe were watching the same entangled pair of particles, and one person decided to change their particle's quantum state, the other person would be able to instantaneously see their own particle react to this change, seemingly far quicker than the speed of light would allow. To EPR, this seemed physically impossible, and they concluded that quantum mechanics must be incomplete.
The idea of quantum entanglement, later described by Einstein as “spooky action at a distance,” initiated a new approach towards the common understanding of quantum mechanics. For several decades after the release of the paper, a leading theory pointed to the existence of some set of “hidden variables” that explain this behavior.
This wouldn’t be seriously challenged until 1964, when Northern Irish-born physicist John S. Bell was working at the University of Wisconsin-Madison while on leave from the European Council for Nuclear Research (CERN). Bell happened to stumble across EPR’s 1935 paper and, upon reading its interpretation of quantum entanglement and hidden variables, Bell used relatively simple statistical principles to derive the set of inequalities that would famously go on to later be known as the Bell Inequalities.
Bell published his work in a paper titled “On the Einstein Podolsky Rosen Paradox.” Its contents were dedicated to carefully setting up the momentous inequalities. Roughly summarized, the Bell Inequalities were able to show that it was in fact possible to “detect” the presence of quantum hidden variables, all without knowing what they were.
If hidden variables were really behind quantum entanglement, then Bell’s Inequalities would hold true — proving the EPR interpretation right. However, if it could statistically be shown that the inequalities were not valid, then it could be seen as evidence that the original understanding of quantum entanglement is in fact correct.
Bell, for his part, believed the latter — that the inequalities would be violated — thus solidifying the previous understanding of quantum mechanics. For the time being, however, Bell would have to wait for this confirmation.
Several years later, John Clauser, a then postdoc at the University of California-Berkeley, discovered Bell’s work and began thinking about the experiment that would ultimately become the first of this year’s Nobel winning trio.
To complete this experiment, Clauser constructed an instrument that could measure the variables Bell’s Inequalities demanded. To the surprise of many, Clauser’s experimental data violated a Bell Inequality, marking the first step in proving the “spooky action” introduced by EPR 30 years earlier.
John S. Bell passed away in 1990, leaving him unable to see the most recent progress his work enabled. However, the mathematics he left behind cemented their place as a vital and foundational piece of this year’s Nobel Prize in Physics.